자료구조 기록의 마지막! 트리에 대해서 기록해보자!

📕트리(Tree) 개념
트리는 위의 바오밥 나무를 뒤집은 구조라고 생각하면 이해하기가 쉽다. 구조가 나무와 닮아 있기 때문에 Tree라고 이름을 부텼다. 하나의 뿌리에서 가지가 사방으로 나오는 모습을 하고 있다. 트리 구조는 노드(또는 Vertex라고도 한다.)가 부모 자식의 관계를 가지는 구조이다. 제일 상단에 있는 노드를 root라고 하고, 더이상 자식의 노드가 없는 노드는 나뭇잎과 같기 때문에 leaf라고 합니다. 그리고 같은 부모 노드에 붙어있는 자식노드를 묶어서 부를 때는 sibling node 형제 노드라고 합니다.

🌳트리의 종류
트리에는 종류들이 많이 있고, 또 형태에 따라서 나뉘기도 한다. 완전이진트리, 정 이진트리, 포화이진트리, 그리고 balanced 한지 unbalanced한지 나뉘어 있다. 하지만 나는 이진트리와 이진 검색트리를 기록할 예정이다.
1. 이진트리(Binary Tree)
이진트리는 노드가 하나 이상의 자식을 가지면 트리라고 하는데, 자식 노드가 최대 2개까지 붙는 노드를 이진트리라고 한다.

물론 노드가 꼭 2개만 붙으라는 법은없다 3, 4개가 붙은 트리도 있지만, 오늘은 이진트리와 이진 검색트리만 기록한다! 이진트리는 따로 조건 없이 구성되어 있다. 하지만 다음에 기록하는 이진 검색트리는 특정한 조건이 존재하고 있다.
2. 이진 검색트리(Binary Search Tree)
이진 검색트리는 안에 있는 데이터가 왼쪽 노드와 그 이하 자식 노드는 현재노드보다 작아야 하고, 오른쪽과 그 이하 자식 노드들은 현재노드 보다 커야한다. 이해가 쉽게 되지 않기 때문에 사진으로 살펴보자.

현재의 노드가 15라고 한다면 15보다 작은 노드인 10은 왼쪽에 위치하고, 큰 20은 오른쪽에 위치하는 것을 볼 수 있다. 그리고 10으로 갔을 때는 어떻게 되는지 살펴보자

10으로 내려와서 현재 노드는 10이 되었다. 마찬가지로 6은 10보다 작기 때문에 10의 왼쪽으로, 13은 10보다 크기 때문에 오른쪽에 위치하고 있다.
이진검색트리를 활용하게 되면 내가 찾는 값이 시작하는 현재노드의 값보다 작으면 계속해서 왼쪽으로 탐색을하면 되고, 값이 크다면 오른쪽을 탐색하면 된다.
🔎트리의 탐색
탐색을 하는 방법에는 크게 두가지가 존재한다. 깊이 우선탐색 (DFS), 너비 우선탐색(BFS) 이렇게 2가지가 있다. 그래서 2가지를 그림과 함께 기록해보자!
1. 깊이 우선탐색(DFS : Depth First Search)
깊이 우선탐색은 왼쪽으로 최대한 깊이 내려가다가, 더이상 내려 갈곳이 없는 경우에 옆으로 이동해서 탐색하는 방식이다. 다음 노드에 있는 숫자가 탐색 순서를 나타낸다.

혹시 미로를 탈출하는 게임영상을 본적이 있다면 '오른쪽의 법칙'(솔직히 이런 이름이 있는 법칙인지는 모르겠음...)이라고 있다. 미로를 탈출하기 위해서는 계속해서 오른쪽으로 돌면서 길을 찾다가 보면 언제가는 탈출을 하게 되는 법칙을 말한다. 오른쪽으로 가다가 벽을 마주하게 되면 다시 나오고, 나와서 또 오른쪽을 우선으로 가다 보면 언젠가 탈출구가 나온다.궁굼하시다면.... 직접 해보셔도 됩니다... 마치 깊이 우선탐색이 오른쪽의 법칙과 비슷한 것 같다. 한쪽을 계속해서 파고 들다가 더이상 길이 없으면 나와서 다음쪽으로 가는 것과 유사하다.
2.너비 우선탐색 (BFS : Breadth First Search)
인접한 노드를 먼저 탐색하는 방법이다. 형제노드를 먼저 훑으면서 한칸씩 내려가서 또 그 형제들을 탐색하는 방식이다.
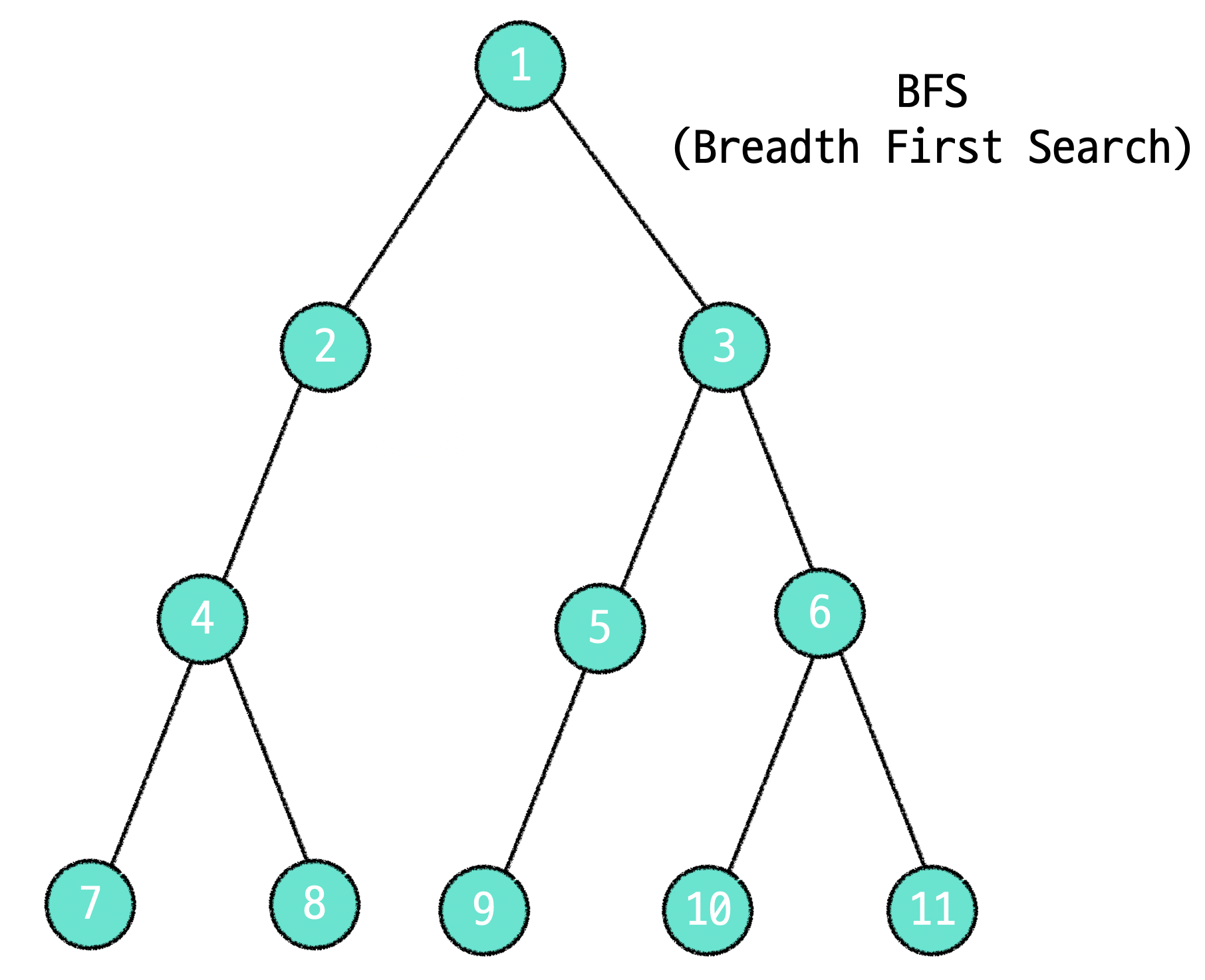
주로 두 노드사이에 가장 빨리 도달할 수 있는 경로를 찾고 싶을 때 이방법을 사용한다. 내가만약 어떤 사람을 찾고 싶다면 나는 그 사람을 찾기위해 친구들한테 찾는 사람에 대해 말을합니다. 그 친구들 선에서도 찾을 수 없으면 친구의 친구한테 연락을 해서 사람을 계속해서 찾는 방식이라 생각하면 좋을 것 같다.
📍트리, 이진탐색트리 메소드
이번 코드스테이츠 스프린트에서 메소드를 구현한것은 다음과 같다.
1. 트리
-
insertNode(value) - 트리에 노드를 추가합니다.
-
contains(value) - 트리에 해당 노드가 존재하는지 여부를 반환합니다.
2. 이진탐색트리
-
insert(value)- 이진탐색 트리에 노드를 추가합니다.
-
contains(value) - 이진 탐색트리에 해당 노드가 존재하는지 여부를 반환합니다.
-
inorder(callback) - 이진 탐색 트리를 중위 순회 합니다.
💻트리, 이진탐색트리 메소드 구현
1. 트리 메소드 구현
class TreeNode {
constructor(value) {
this.value = value;
this.children = [];
}1. 1. insertNode(value)
- 새로운 노드를 new키워드를 사용해서 만들어 준다.
- 만든 노드를 자식 노드에 추가해준다.
1. 2. contains(value)
- 재귀를 활용해서 만들어 주었다.
- 먼저 자식이 해당하는 값을 가지고 있으면 true를 반환한다.
- 그리고 재귀를 활용해서 해당하는 자식들의 값들도 확인해 주었다.
2. 이진탐색트리 메소드 구현
2.1 insert(value)
- 먼저 값의 크기를 비교해준다.
- 값이 작다면 왼쪽으로, 크다면 오른쪽으로 가야한다.
- 만약에 왼쪽으로 갔는데 이미 값이 있다면, 그 값을 다시 비교해주어야 하기때문에 재귀로 작성해 주었다.
2.2 contains(value)
- 재귀를 활용해서 작성해 주었다.
- 먼저 값의 크기를 비교해 주어서 왼쪽으로 갈지 오른쪽으로 갈지 나누어 주었고, 계속해서 비교해주면서 자식 노드들도 확인하도록 작성해 주었다.
2.3 inorder(callback)
- 콜백함수는 이미 코드스테이츠에서 만들어 주었다.
- 중위순회 방식으로 값을 꺼내기 위해서 먼저 왼쪽부에서 값을 순회하고 왼쪽이 끝나면 root를 그리고 오른쪽으로 가서 값을 순회하도록 작성해 주었다.
♻️전위, 중위, 후위 순회
1. 전위 순회
전위 순회는 현재도느에서 시작하여 왼쪽 노드에서 오른쪽 노드로 탐색하는 방식입니다. (현재 -> 왼쪽 -> 오른쪽)

2. 중위 순회
중위 순회는 왼쪽에서 부터 현재노드로 와서 오른쪽 노드로 탐색하는 방식입니다. (왼쪽 -> 현재 -> 오른쪽)
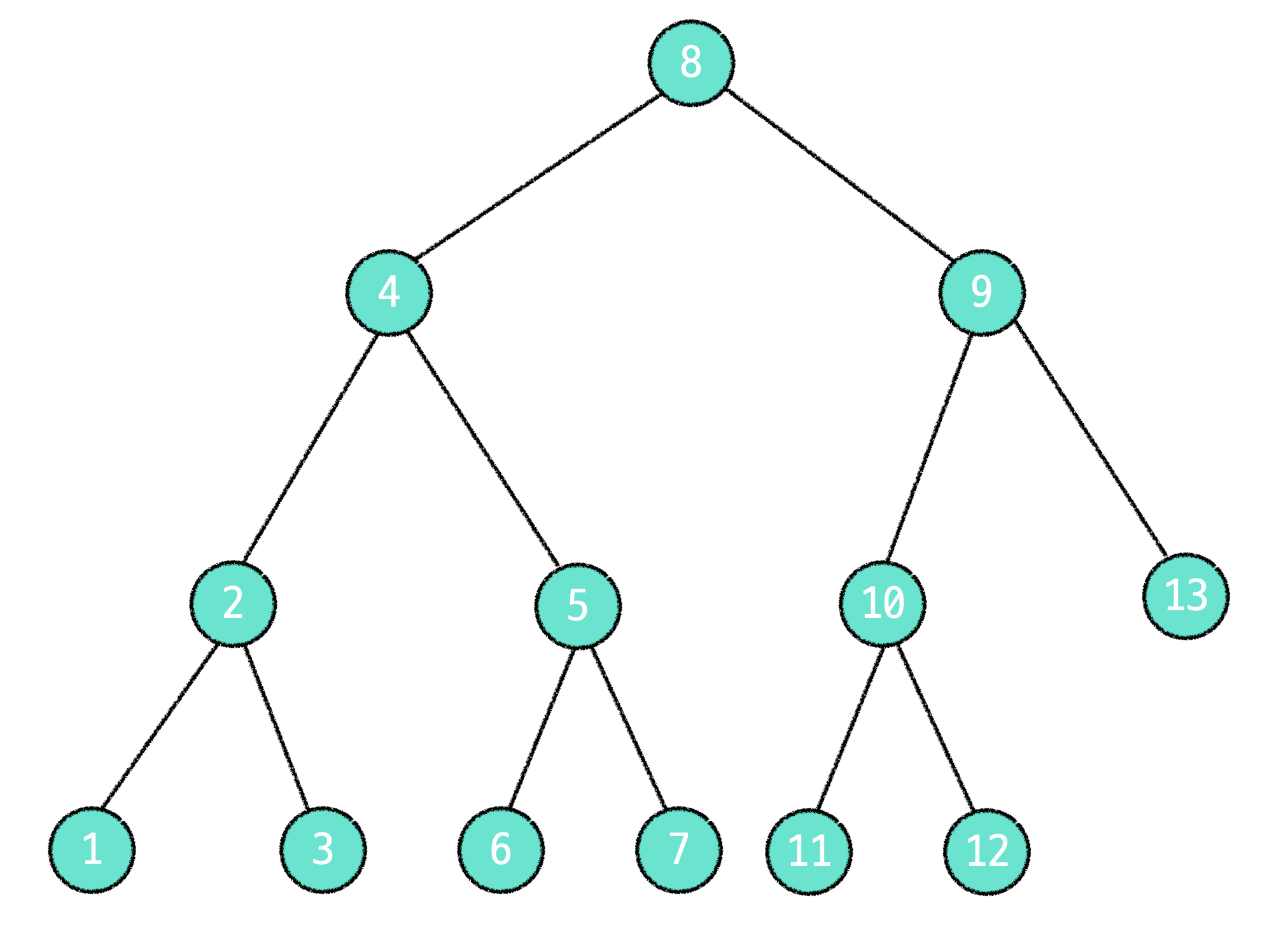
3. 후위 순회
후위 순회는 왼쪽에서 부터 오른쪽 현재로 탐색하는 방식입니다. (왼쪽 -> 오른쪽 -> 현재)

다음은 무엇을 기록해볼까!
'리코딩 : 자료구조(Data Structure)' 카테고리의 다른 글
| 자바스크립트 12. 자료구조(Data Structure) - 그래프 (graph) (0) | 2020.11.06 |
|---|---|
| 자바스크립트 12. 자료구조(Data Structure) - 해시테이블 (Hash Table) (0) | 2020.11.06 |
| 자바스크립트 12. 자료구조(Data Structure) - 연결리스트(Linked List) (0) | 2020.11.05 |
| 자바스크립트 12. 자료구조(Data Structure) - 큐(Queue) (0) | 2020.11.05 |
| 자바스크립트 12. 자료구조(Data Structure) - 스택(Stack) (0) | 2020.11.05 |